Fir wat gi epizyklesch Zännrieder benotzt?

Epizyklesch Zännriederoch bekannt als Planetargetriebesystemer, gi wäit a verschiddene Branchen agesat wéinst hirem kompakten Design, héijer Effizienz a Vielfältegkeet

Dës Zännrieder ginn haaptsächlech a Betriber benotzt, wou de Raum limitéiert ass, awer en héicht Dréimoment a Geschwindegkeetsvariabilitéit essentiell sinn.

1. Automotive Transmissions: Epizyklesch Getrieber sinn eng Schlësselkomponent an automatesche Getrieber, a suergen fir nahtlos Gangwiesselen, en héijen Dréimoment bei niddrege Geschwindegkeeten an eng effizient Kraaftiwwerdroung.
2. Industriell Maschinnen: Si gi a schwéiere Maschinnen agesat fir hir Fäegkeet, héich Laaschten ze handhaben, den Dréimoment gläichméisseg ze verdeelen an effizient a kompakte Raim ze funktionéieren.
3. Loftfaart: Dës Zännrieder spille eng entscheedend Roll a Fligermotoren an Helikopterrotoren a garantéieren Zouverlässegkeet a präzis Bewegungskontroll ënner usprochsvollen Konditiounen.
4. Robotik an Automatiséierung: An der Robotik ginn epizyklesch Getrieber benotzt fir eng präzis Bewegungskontroll, e kompakt Design an en héicht Dréimoment a limitéierte Plazen z'erreechen.

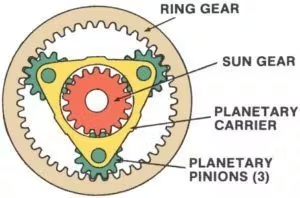
Wat sinn déi véier Elementer vum epizyklische Getriebe-Set?

En epizyklesche Zännradsatz, och bekannt alsPlanéitenzahnrad System, ass e ganz effizienten a kompakte Mechanismus, deen dacks an Autosgetrieber, Robotik an industrielle Maschinnen benotzt gëtt. Dëst System besteet aus véier Schlësselelementer:

1. SonnenausrüstungD'Sonnenzännrad ass an der Mëtt vum Zännrad positionéiert an ass den Haaptantrieb oder Empfänger vun der Bewegung. Et wierkt direkt mat de Planéitenzännrieder a déngt dacks als Input oder Output vum System.

2. PlanéitenzahnräderDëst sinn e puer Zännrieder, déi ëm de Sonnenzandrad dréien. Si sinn op engem Planéitenträger montéiert a stinn a Kontakt souwuel mam Sonnenzandrad wéi och mam Rankzandrad. D'Planéitenzännrieder verdeelen d'Laascht gläichméisseg, sou datt de System en héijen Dréimoment veraarbechte kann.

3.PlanéitenträgerDës Komponent hält d'Planéitrad op der Plaz an ënnerstëtzt hir Rotatioun ëm d'Sonnerad. De Planéitendréier kann jee no der Konfiguratioun vum System als Input-, Output- oder stationärt Element déngen.

4.ZännradDëst ass e grousst äussert Zännrad, dat d'Planéitzännrad ëmschléisst. Déi bannenzeg Zänn vum Rankrad interagéiere mat de Planéitzännrad. Wéi déi aner Elementer kann de Rankrad als Input, Output déngen oder stationär bleiwen.

D'Zesummespill vun dëse véier Elementer bitt d'Flexibilitéit fir verschidden Geschwindegkeetsverhältnisser a Richtungsännerungen an enger kompakter Struktur z'erreechen.

Wéi berechent een d'Geschwindegkeet vum Austauschverhältnis an engem epizyklischen Zännrad?

D'Geschwindegkeetsverhältnis vun engemepizyklesch Getriebesatz hänkt dovun of, wéi eng Komponenten fix sinn, Input an Output. Hei ass eng Schrëtt-fir-Schrëtt-Anleitung fir d'Berechnung vum Getriebeverhältnis:

1. D'Systemkonfiguratioun verstoen:

Identifizéiert wéi ee Element (Sonn, Planéitendréier oder Rank) stationär ass.

Bestëmmt d'Input- an d'Output-Komponenten.

2. Benotzt d'Grondverzënsungsgläichung: D'Verzënsungsverhältnis vun engem epizyklesche Getriebesystem kann mat folgendem berechent ginn:

GR = 1 + (R / S)

Wou:

GR = Gangverhältnis

R = Zuel vun den Zänn um Rankrad

S = Zuel vun den Zänn um Sonnenzännrad

Dës Equatioun gëllt wann de Planéitendréier d'Ausgab ass, an entweder d'Sonn oder de Rankrad stationär ass.

3. Upassen fir aner Konfiguratiounen:

• Wann de Sonnenrad stationär ass, gëtt d'Ausgangsgeschwindegkeet vum System vum Verhältnes vum Rankrad an dem Planéitendréier beaflosst.
• Wann de Rankrad stationär ass, gëtt d'Ausgangsgeschwindegkeet duerch d'Bezéiung tëscht dem Sonnenrad an dem Planéitendréier bestëmmt.

4. Réckwärtsgangverhältnis fir Ausgang zum Input: Bei der Berechnung vun der Geschwindegkeetsreduktioun (Input méi héich wéi Output) ass d'Verhältnis einfach. Fir d'Geschwindegkeetsmultiplikatioun (Output méi héich wéi Input), dréit dat berechent Verhältnis ëm.

Beispillberechnung:

Stellt Iech vir, datt e Gangsatz huet:

Rankzahnrad (R): 72 Zänn

Sonnenzännrad (S): 24 Zänn

Wann de Planéitenträger d'Ausgab ass an d'Sonnenzännrad stationär ass, ass d'Gearverhältnis:

GR = 1 + (72 / 24) GR = 1 + 3 = 4

Dëst bedeit datt d'Ausgangsgeschwindegkeet 4 Mol méi lues ass wéi d'Inputgeschwindegkeet, wat e Reduktiounsverhältnis vu 4:1 ergëtt.

D'Verständnis vun dëse Prinzipien erlaabt et Ingenieuren, effizient a villfälteg Systemer ze entwéckelen, déi op spezifesch Uwendungen zougeschnidden sinn.